


































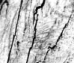




















Matlab source: synth.m
Efros & Leung's algorithm is remarkably simple. First, initialize a synthesized texture with a 3x3 pixel "seed" from the source texture. For every unfilled pixel which borders some filled pixels (I think of this as a pixel on the 'frontier'), find a set of patches in the source image that most resemble the unfilled pixel's filled neighbors. Choose one of those patches at random and assign to the unfilled pixel a color value from the center of the chosen patch. Do this a few thousand times, and you're done. The only crucial parameter is how large of a neighborhood you consider when searching for similar patches. As you can see in the examples below, as the "window size" increases, the resulting textures capture larger structures of the source image. If you want to implement this algorithm, there are some finer details you should read about in the paper linked below.
I implemented this as a homework for Rob Fergus' Computational Photography class. If you're interested in this sort of thing, check out the course website, which has many more interesting papers.
Reference: Texture Synthesis by Non-parametric Sampling
| Source | 3 x 3 window | 5 x 5 window | 7 x 7 window | 11 x 11 window | 15 x 15 window | 19 x 19 window |
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Matlab source: synth_gmm.m, EM_GM.m
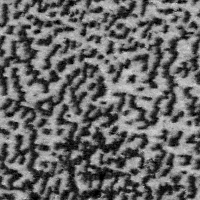
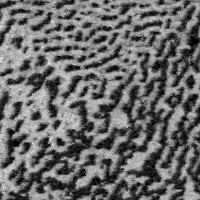
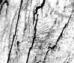
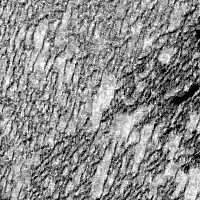
I started from Efros & Leung's algorithm and rewrote it to use an explicit patch density model. Instead of measuring the distance from the current synthesized patch to every patch in the original image, I sample a few patches from a Gaussian mixture model and use the sample with lowest distance. This trades a terrible start-up cost (waiting for EM to converge) for a much quicker per-pixel running time. If the visual performance were comparable, this scheme would be well-suited for synthesizing large textures. Unfortunately, the results from the mixture model don't look so great. When I have time, I'm hoping to try this with a Restricted Boltzmann Machine.
| Source | 3 x 3 window | 5 x 5 window | 7 x 7 window | 11 x 11 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
|
 |
 |
 |
 |
|
 |
 |
 |
 |
|
 |
 |
 |
 |